かめ(管理人の一人)は音楽の教養が全くありませんが、ミュージシャンになることを夢見ています。
今回は音楽の始めるための切り口として、ギターコードや五度圏表の仕組みを調査・考察した結果を記録に残します。
※かめがミュージシャンを夢見るようになった経緯はこちらの記事で紹介しています。
ギターコードと五度圏表について
音楽の素人のかめは何から音楽の勉強を始めればよいのかよく分からなかったので、身近なギターを利用して、
【ギターコード】
の仕組みを調査することにしました。
ギターコードは特定の和音を手軽に演奏できる一方で、何の音が組み合わされているのか直感的に理解しずらいところがありましたので、
まずは、ピアノの鍵盤の並びからギターコードの和音の構成を理解したいと考えていました。
そこで、「ギターコード ピアノコード 違い」のキーワードでGoogle検索しましたところ、
作編曲家・シンガーソングライター・歌のお兄さんの渡部絢也さんのサイトが検索上位でヒットしました!!
★サイトリンク:https://watanabejunya.com/what-chord/
かめが知りたかった数多くの情報がとても分かりやすく、かつ、綺麗にまとめられています!!
Brilliant!!!
以下の点は、渡部絢也さんのサイトの「おいでよ!作曲初心者」シリーズを、サッと読んでみてかめが理解できたポイントです。
※詳細はサイトをのぞいてみることをオススメします!
<かめが理解できたポイント>
- ギターコードとピアノの鍵盤の配置や楽譜上の音符の関連性。(自分で整理する手間が省けた。)
- 曲にはベースとなる音があり、それが決まることで【曲を構成する7つの基本の音】も決まる。
- メロディの音やギターコードはその7つの音で基本的に構成されている。
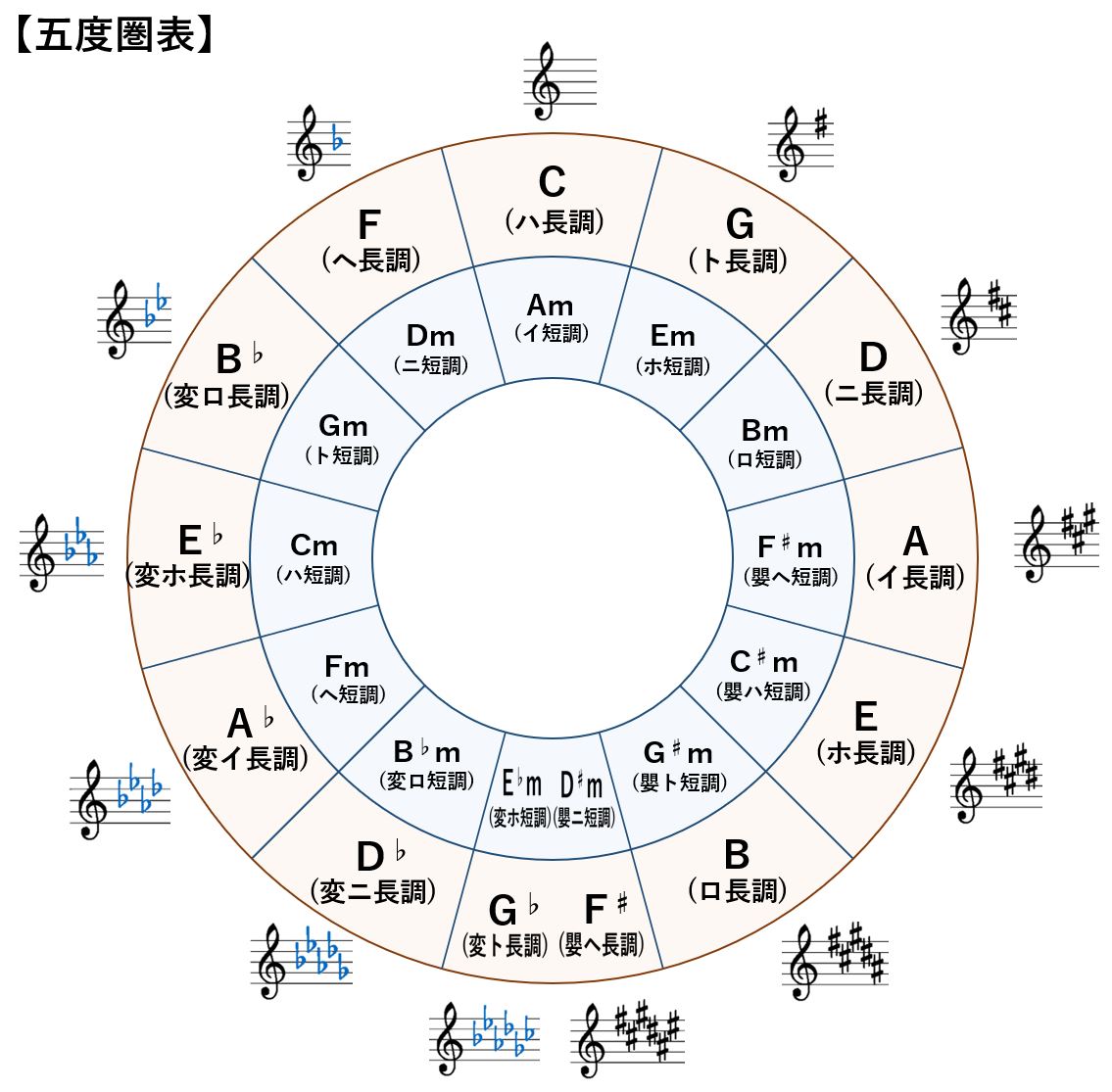
- 【五度圏表】を利用することで、組み合わせの良いコードが一目で分かる。
この時かめは初めて【五度圏表】なるものに出会ったのですが、
「ミュージシャンになるにはまずこれを知っておかなければならない」
と直感的に理解しました!
【五度圏表】が何なのか調査・考察を進めてみます。
五度圏表とは
【五度圏表】やその使い方は渡部絢也さんのサイトに詳しく書かれていますが、ここではかめがWikipediaの【五度圏】のサイトやそこから派生するリンク先の情報も読み込んで、解釈した内容を記録していきます。
※Wikipediaの【五度圏】のリンクはこちら。
https://ja.wikipedia.org/wiki/%E4%BA%94%E5%BA%A6%E5%9C%8F
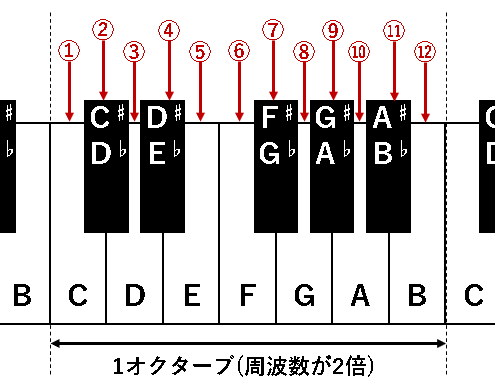
1.1オクターブを構成する音は12つに分割されている。
ピアノの鍵盤で表すと、ドレミファソラシドの7つと5つの半音が1オクターブ中に存在します。
現代ではピアノの調律は、【十二平均律】によって行われているため、半音を含めた隣り合う鍵盤は、【2の12乗根】¹²√2倍だけ周波数が大きいか小さいかの関係にあります。
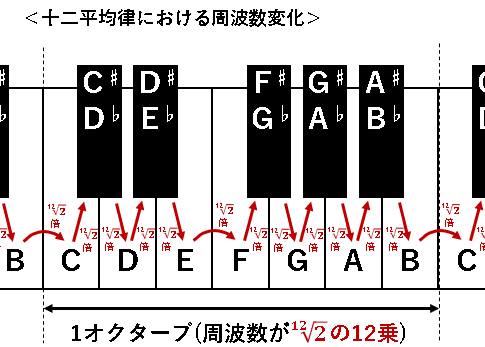
¹²√2倍を12回掛け算すると元の音の周波数が2倍になり、音程が1オクターブ高くなる仕組みになっています。(割り算すると逆に1オクターブ低くなる。)
2.完全五度の関係は音の親和性が高い。
【完全五度】と呼ばれる関係にある音同士を隣り合わせにしてこれらを並べると【五度圏表】の原形ができあがります。
※完全五度:十二平均律において、ピアノの鍵盤上で隣り合う鍵盤を半音も含めてすごろくのように7回進んだ先にある音との関係。
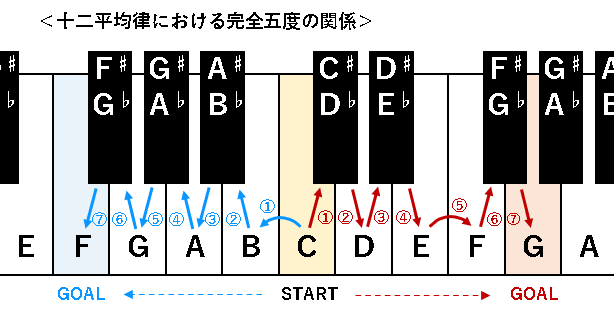
この【完全五度】の関係にある音同士は、周波数がおよそ1.5倍(3/2倍)の関係にあるため音の親和性が高いと言えます。
ゆえに、隣り合う【完全五度】の音同士をベースとしたコード(和音)を組み合わせて作曲すれば、安定感のある曲に仕上がるようです!
※隣の隣はそこまでよろしくないようです…
試しに1.5倍した音の波と¹²√2倍を6回掛け算した(=√2倍した)音の波をそれぞれ元の音の波に同じ振幅で重ね合わせたグラフを描いてみます。
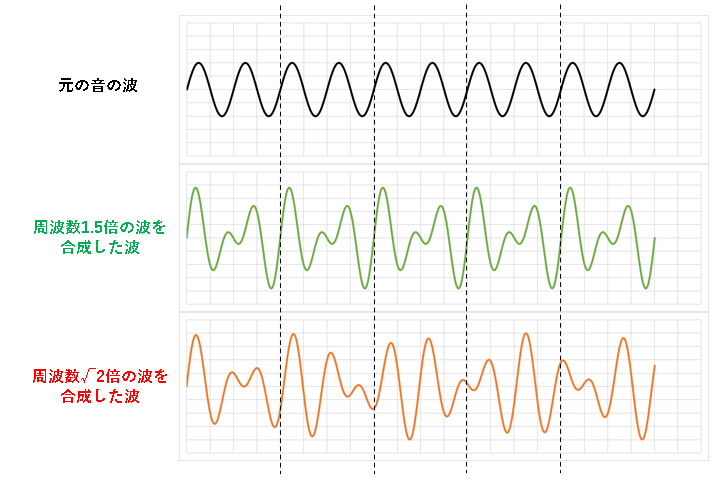
波形はどちらも似ていますが、1.5倍した波を重ね合わせた場合に周期的に同じ波形が見られるのに対して、√2倍した波を重ね合わせた場合では、周期的な波形がすぐには見つかりません。
音の波形や周波数といった科学的な観点からは、綺麗な整数倍で分割されている【完全五度】やオクターブの音の組み合わせの方が、心地よく聞こえるのだと理解しました。
この点について細かい話をすると、【五度圏表】の下のG♭とF♯はピアノの鍵盤上では同じ音程ですが、あえて分けられて書かれています。
これは【ピタゴラス音律】における【完全五度】のルールに従ってG♭から周波数を12回正確に1.5倍し続けた時に、G♭と7オクターブ上のF♯が同じ音程にならないためです。
- 【十二平均律】における7オクターブ上は、2の7乗で128倍の周波数
- 【ピタゴラス音律】における【完全五度】の1.5倍を12回繰り返すと129.74倍の周波数(7オクターブをやや行き過ぎている)
- 高音から低音まで広い音域に渡って演奏した時に、音程のずれが発生することから、【十二平均律】によるピアノのチューニングが現在の標準となっている。
なお、【十二平均律】における【完全五度】は、先ほどおよそ1.5倍と記したように実際には1.4983倍に微調整されているため、整数の比できれいに分割されていない音程に違和感を感じる人もいるようです。
【五度圏表】の下のG♭とF♯が分けられている理由は、なかなか興味深かったので、忘れないように少し深堀りしてみました♪
3.マイナーと呼ばれる音の組み合わせにも親和性が高いものがある。
【五度圏表】の内側には、冒頭で環状に並べた12個の音が【マイナー】と呼ばれる形で配置されています。
これらは外側に並べられた12個の【メジャー】と呼ばれる音に対して、隣り合う鍵盤を半音も含めてすごろくのように3回戻った位置にある音が対応しています。
この3回戻った位置の音の波を合成したところ、【完全五度】の音との合成に比べて周期が3倍長いうなりが発生しているのが分かります。
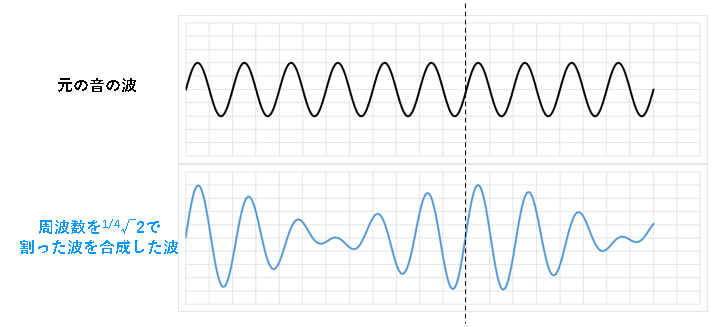
想像でしかないですが、【完全五度】の音ほど相性は良くないけれど一緒に使えないこともないといったところでしょうか…?
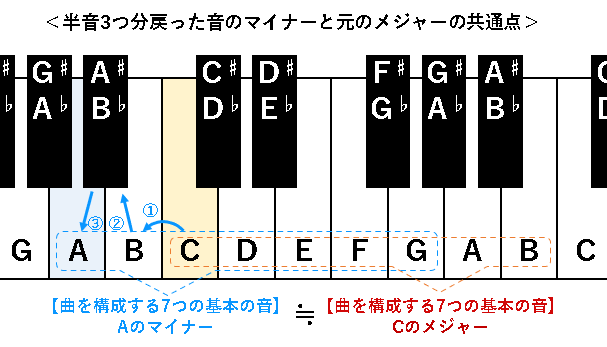
一方で、【曲を構成する7つの基本の音】に注目すると、元の音の【メジャー】と構成が同じとなっており親和性が高いと考えられます!
- 【メジャー】は日本語の「~長調」に相当し、明るめの曲調となる。
【曲を構成する7つの基本の音】は半音を1とすると、「2→2→1→2→2→2→1(戻り)」の離隔関係となっている。 - 【マイナー】は日本語の「~短調」に相当し、暗めの曲調となる。
【曲を構成する7つの基本の音】は半音を1とすると、「2→1→2→2→1→2→2(戻り)」の離隔関係となっている。 - 【メジャー】の音の並びを半音3つ分巻き戻すと【マイナー】の並びになっていることが分かる。
- 【曲を構成する7つの基本の音】は、楽譜のト音記号の右についている♯や♭の数で判断することができ、【五度圏表】に記載されているように12種類に分類されている。
また、この12種類に長調と短調が1つずつ存在する。
楽譜のト音記号の右についている♯や♭の数と、長調と短調にそんな関連性があったことを知り、とても勉強になりました!!
確かに、クラシック曲でよく表記されている「~長調」や「~短調」と、楽譜の♯や♭の数の関係を見てみると見事に合致していました!
また、日本のポップやロックのバンドスコアやギターのコード譜を見ても、ほとんどこの規則性に従っていることが分かりました!
【五度圏表】に記載されている【マイナー】の部分も、お隣さんは【完全五度】の関係にありますので、【メジャー】と同じ親和性を期待してもよいようですね。
【五度圏表】があれば残業まみれのサラリーマンでも作曲できそうな気分になりますね!(笑)
五度圏表で音楽の嗜好をチェック
音楽のことが素人なりにいろいろ勉強になったところで、早速、この【五度圏表】を使って遊んでみることにしました。
かめが好きな日本のポップやロックの曲と、つるさん(もう一人の管理人)が好きなクラシックの曲を【五度圏表】に落とし込んでみます!
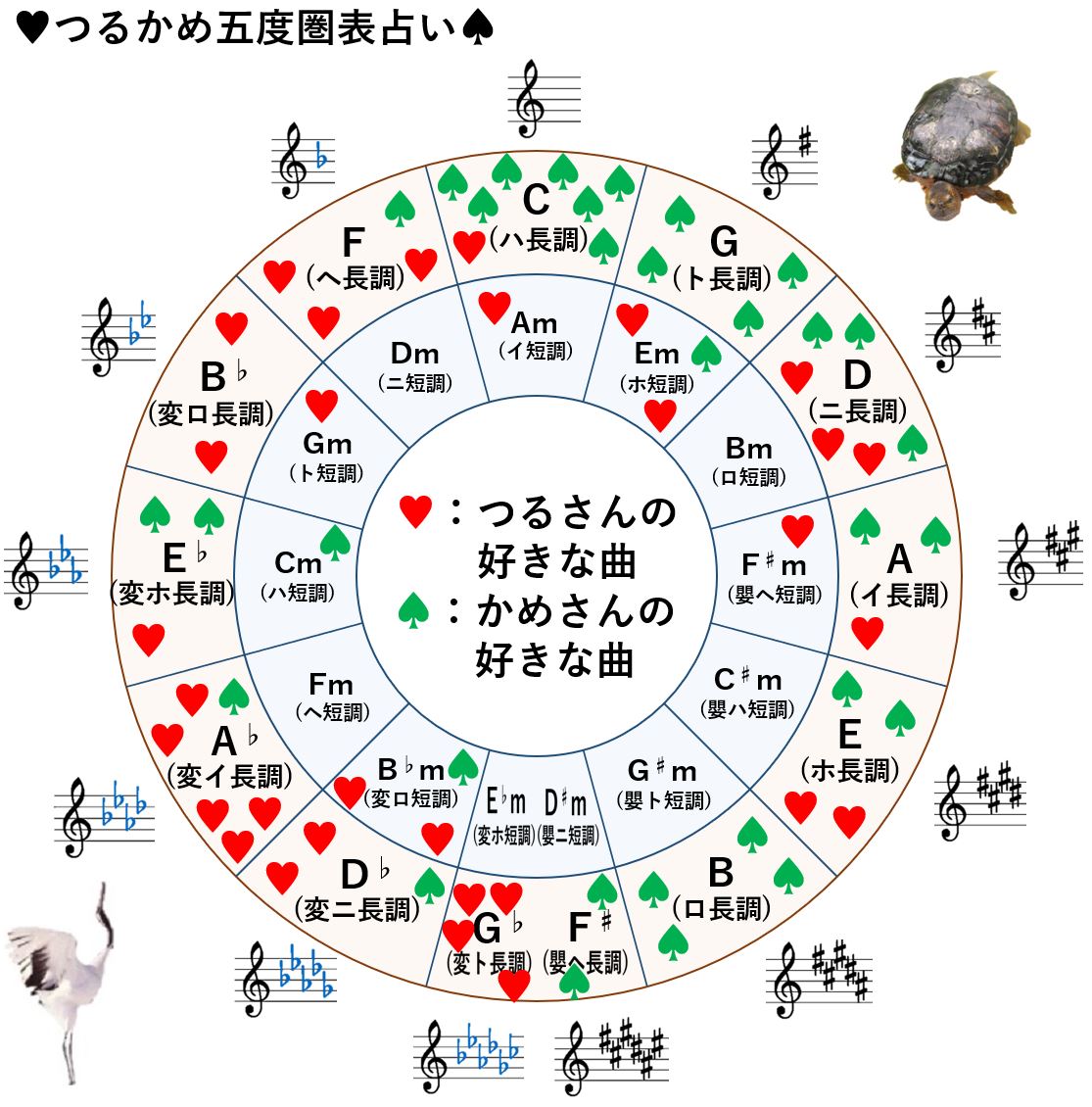
かめの予想通り、かめの好きな曲は特定の曲調に偏っています!
そして、こちらも予想していた通り、
つるさんの好きな曲はかめの好きな曲の反対側に偏っています(笑)
以前から曲の嗜好が違うことは認識していたので、話題としてとても盛り上がりました(笑)
その時に好きな曲の調を調べることで、精神状態の占いができそうですね♪
少し安心したのが、両者とも【メジャー】の曲の方が圧倒的に多かった点です。
かめにとっては音楽は、
自分のノリを増幅させる【エネルギー源】
ですので、【マイナー】の曲でますますしみじみしてしまうのはよろしくない傾向だと思います。
元気で明るい曲をたくさん作曲して、定年退職までのサラリーマン生活を乗り切りたいと思います!!
関連記事
【つるかめ五度圏表占い】を毎年更新することにしました(笑)


